一、题目
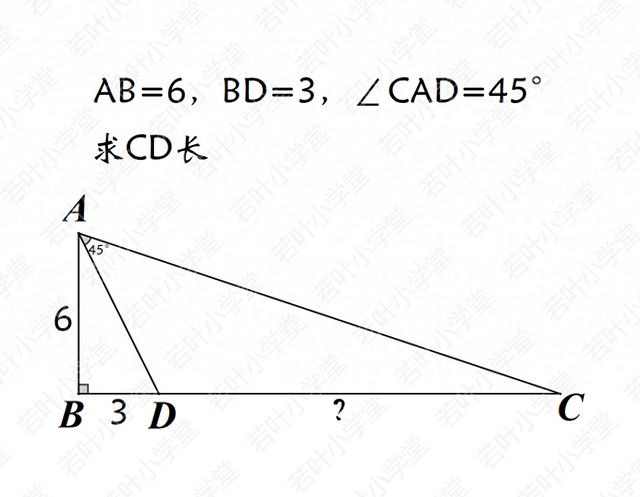
在Rt△ABC中，D是BC上一点，BD=3，AB=6，∠CAD=45°，求CD的长.
二、分析与解答
本题的核心条件是45°角，要解决本题，那就要深挖45°角.
看到45°角你会想到什么？
∠CAD=45°，tan∠BAD=1/2，你会不会想到12345模型？
遇特殊角，构造特殊三角形，你会不会想到构造等腰直角三角形？你能想到几种构造方法？
再从结果考虑，求线段长常用勾股、相似或三角.
前后结合，无论你的方法简单或复杂，是不是已经有了大概思路了？
解法一：12345模型
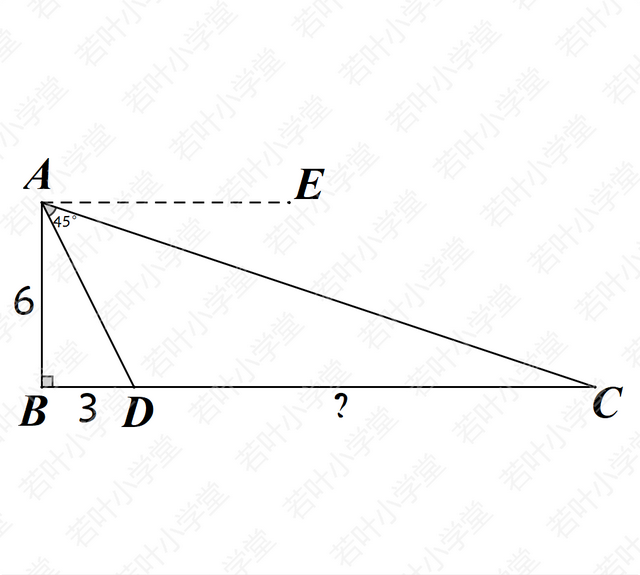
12345模型其实是不需要作辅助线的，但是为了更好地理解，可以过点A作AE//BC
由tan∠BAD=1/2，∠CAD=45°，可以直接得出tan∠BAC=3
如果你对这个结论不熟悉，作辅助线后可以更好地理解.
∠C+∠BAD=∠CAE+∠BAD=45°
再或者由∠BAD+45°+∠C=90°得到∠BAD+∠C=45°
由12345模型，可得 tan∠C=1/3
无论是由tan∠BAC=3或tanC=1/3，均可得到BC=3AB=18
∴CD=BC-BD=15
口诀内乘法，20以内减法，就两步，前提是你要对12345模型熟悉.
解法二：以AD为斜边构造等腰直角三角形，利用相似求解
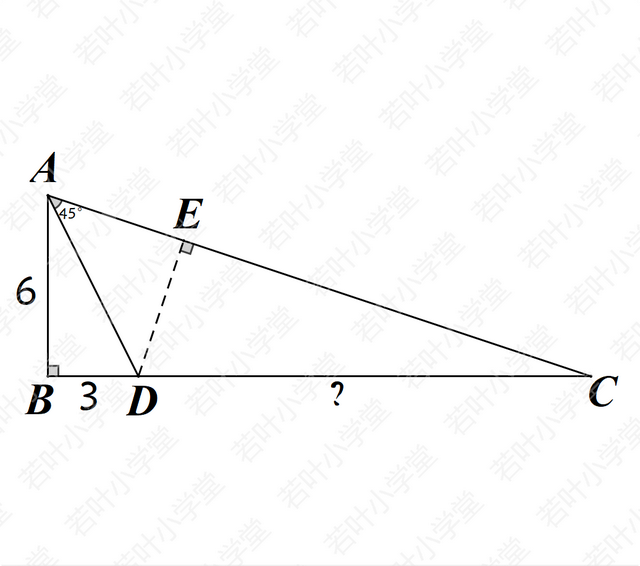
AD=√5BD=3√5，AE=DE=AD/√2=3√10/2
设CD=x，CE=y
易证△CDE∽△CAB ∴DE/AB=CD/CA=CE/CB
即3√10/2:6=x:(3√10/2+y)=y:(x+3)
整理，得√10/4=2x/(3√10+2y)=y/(x+3)
消去y，解得x=15 ∴CD=15
解法三：以AD为斜边构造等腰直角三角形，利用三角函数和勾股定理求解
辅助线同解法二
AD=√5BD=3√5，AE=DE=AD/√2=3√10/2，设CD=x
tanC=AB/BC=DE/CE，即6:(x+3)=3√10/2:CE，CE=√10/4(x+3)
在Rt△CDE中，由勾股定理，得
(3√10/2)^2+[√10/4(x+3)]^2=x^2 解得x=15（取正）∴C=15
解法四：以AD为直角边构造等腰直角三角形，然后构造三垂直全等和A字相似
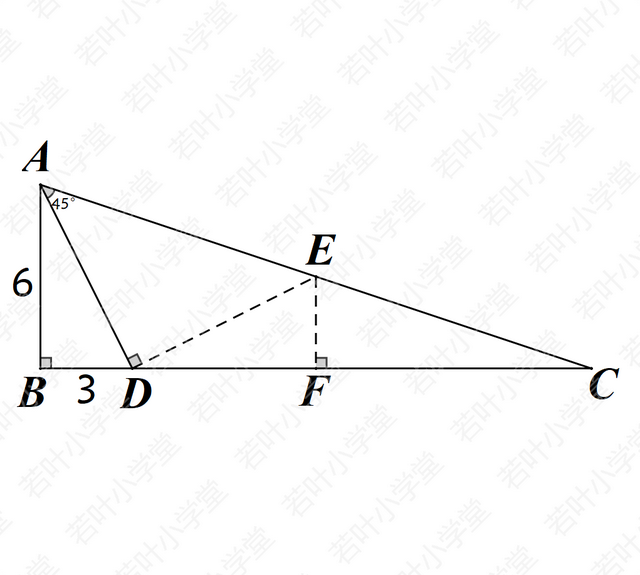
易证△ABD≌△DFE，∴EF=3，DF=6
易证△CEF∽△CAB，∴CF/CB=EF/AB
即CF/(CF+9)=3/6，CF=9，CD=15
解法五：以AC为斜边构造等腰直角三角形
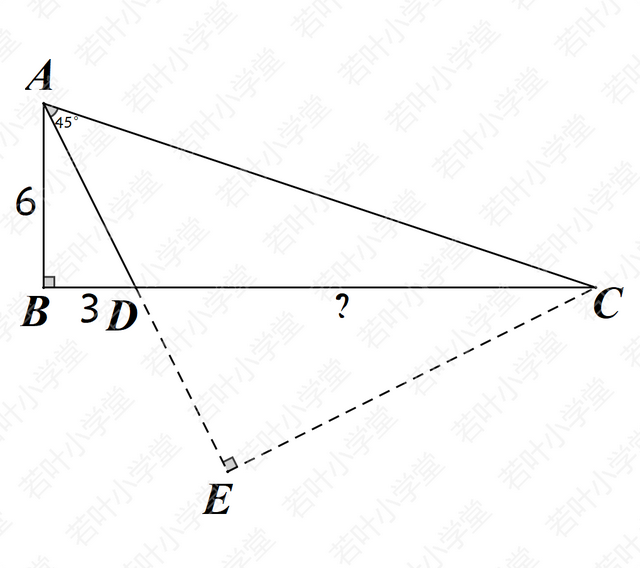
易证△ABD∽△CED
设DE=x，则CE=AE=2x，AD=x=3√5
∴CD=√5DE=15
解法六：以AC为直角边构造等腰直角三角形，解三角形
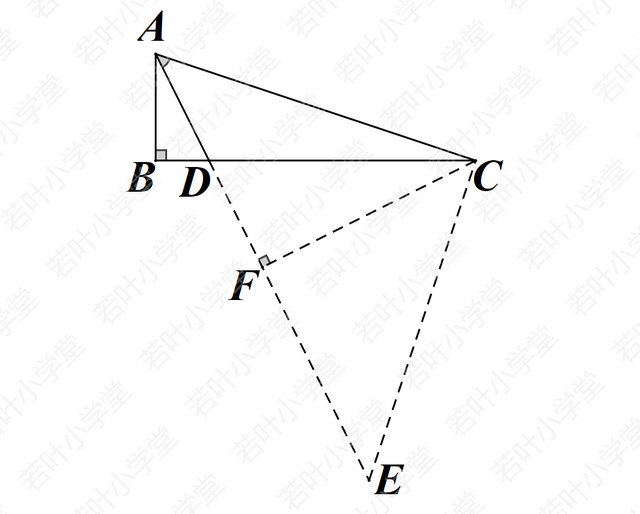
△CDE中，tan∠CDF=2，tan∠CEF=1，DE=√2CE-3√5
设DF=x，则CF=EF=2x，CE=2√2x
∵DE=√2CE-3√5 ∴3x=4x-3√5，x=3√5
∴DF=3√5，CF=6√5，CD=15
三、小结
1、12345在解决填空压轴题时还是很有用的，有必要了解一下.
2、遇特殊角，构造特殊三角形，不同的构造方法难易程度略有不同.
3、求线段长，常用勾股、相似或三角函数，本题虽简单，但三种方法均有体现.
正规股票配资网提示：文章来自网络，不代表本站观点。
- 上一篇：10大配资公司然后再陆续发给老旧机型升级
- 下一篇：没有了
